- 核心概念:路径规划 vs. 轨迹跟踪
- 路径规划
- 目标
- 分类
- 常用算法
- 评价指标
- 轨迹跟踪
- 目标
- 核心挑战
- 常用控制方法
- 两者的关系与协同工作
核心概念:路径规划 vs. 轨迹跟踪
可以这样理解:
(图片来源网络,侵删)
-
路径规划:“从A点到B点,走哪条路?”
- 它关注的是空间,不考虑时间。
- 输出:一条从起点到终点的几何路径(一系列的坐标点或曲线)。
- 在地图上,规划出一条避开障碍物的、最短的或最平滑的路线。
-
轨迹跟踪:“如何精确地沿着那条路走?”
- 它关注的是空间和时间的结合。
- 输入:一条由路径规划生成的(或期望的)轨迹。
- 输出:机器人的实际运动(如线速度
v和角速度 ),使其在特定时间点精确地到达轨迹上的目标点。 - 机器人需要以
5m/s的速度,在t=5s时精确到达路径上的(x, y, θ)点。
一个形象的比喻: 想象你开车导航。
- 路径规划:地图App为你规划出一条从家到公司的路线,告诉你“先上高架,然后在第三个路口下高架,最后右转”,这只告诉你路怎么走。
- 轨迹跟踪:你实际开车时,手握方向盘,控制油门和刹车,让你的车轮精确地沿着导航路线行驶,并且在正确的车道、以合适的速度过弯,这是你执行驾驶指令的过程。
路径规划
目标
- 安全性:避开所有静态和动态障碍物。
- 最优性:通常指路径最短、时间最短、能耗最低或转向最平滑。
- 完整性:如果存在可行解,算法必须能找到它。
- 平滑性:路径应尽可能平滑,便于后续的轨迹跟踪,避免机器人频繁启停或急转弯。
分类
-
基于地图:
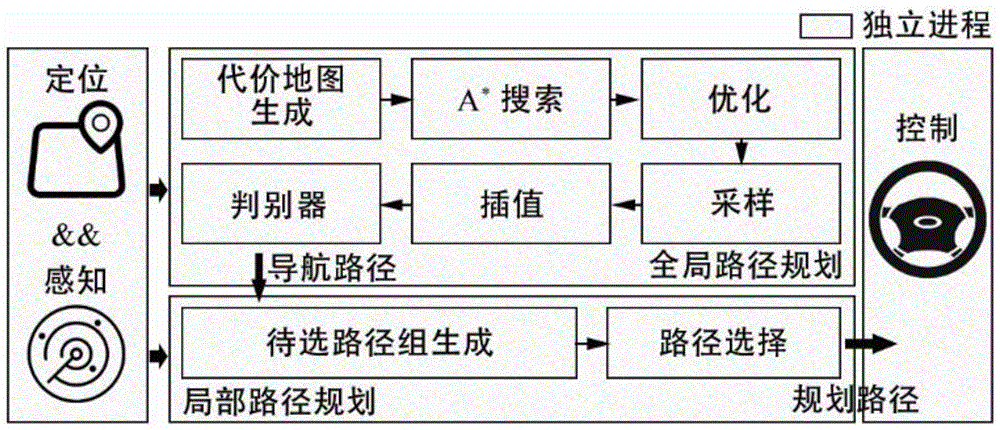 (图片来源网络,侵删)
(图片来源网络,侵删)- 全局路径规划:在已知、静态的环境中进行,拥有完整的先验地图(如栅格地图、拓扑地图),目标是找到一条全局最优路径。
- 局部路径规划:在未知或动态的环境中,根据传感器(如激光雷达、摄像头)的实时信息,在机器人周围的小范围内进行规划,主要用于避障和局部路径调整。
-
基于搜索:
- 在离散的地图(如栅格地图)上进行搜索。
- 经典算法:Dijkstra(保证最短路径,但效率较低)、A*(启发式搜索,效率更高,是应用最广泛的算法之一)。
-
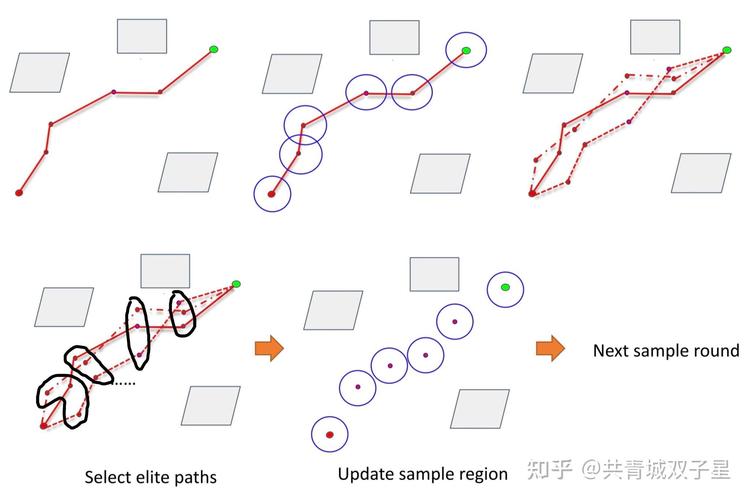
基于采样:
- 在高维或连续空间中随机采样,构建路径图。
- 经典算法:PRM(Probabilistic Roadmap,概率路图法,适用于静态高维空间)、RRT(Rapidly-exploring Random Tree,快速扩展随机树,非常适合处理高维空间和复杂约束,能快速找到可行解,但不保证最优)。
-
基于优化:
- 将路径规划问题转化为一个优化问题(如最小化总长度、最小化控制量、最小化曲率变化等)。
- 经典算法:人工势场法(简单易实现,但容易陷入局部最优)、贝塞尔曲线/B样条曲线(用于生成平滑的路径,常用于工业机器人)。
常用算法举例
- A* 算法:结合了Dijkstra的准确性和贪心算法的效率,通过一个启发函数(如到终点的直线距离)来指导搜索方向,优先探索更有可能找到最优路径的节点。
- RRT 算法:从起点开始,在空间中随机采样一个点,并从当前树中找到离该点最近的节点,向该点方向延伸一小段距离,形成新节点,重复此过程,直到树的分支接近终点,非常适合处理狭窄通道和复杂障碍物。
轨迹跟踪
目标
使机器人的实际状态(位置、姿态)尽可能快、尽可能准确地跟踪上期望的轨迹。

(图片来源网络,侵删)
核心挑战
- 模型不确定性:机器人的动力学模型(如电机响应、摩擦力)与实际存在差异。
- 外部扰动:地面不平、摩擦力变化等。
- 约束条件:机器人的最大速度、最大加速度、最大转向角等。
- 非完整性约束:对于差速驱动机器人,它不能像汽车一样原地平移,只能前进和转弯。
常用控制方法
轨迹跟踪本质上是一个控制问题,其核心是设计一个控制器,根据机器人的当前状态和期望状态,计算出控制指令(v, )。
-
PID 控制
- 原理:最经典、应用最广的控制器,通过计算当前状态与期望状态的误差,然后根据误差的比例、积分、微分项来计算控制输出。
- 优点:结构简单,易于理解和实现。
- 缺点:参数整定需要经验,对于非线性系统(如机器人运动)效果可能不佳,容易产生超调和振荡。
-
纯追踪算法
- 原理:一个非常直观且有效的算法,它假设机器人是一个点,从机器人当前位置看向前方一定距离(称为前视距离 Look-Ahead Distance),期望轨迹上那个点被称为目标点,机器人计算一个转向角,使其朝向该目标点前进。
- 优点:实现简单,对于非完整约束的移动机器人效果很好。
- 缺点:前视距离的选择对性能影响很大,需要根据速度动态调整。
-
线性化控制
- 原理:在机器人当前位姿附近,将非线性的运动学模型进行线性化,然后设计线性控制器(如LQR - 线性二次调节器)。
- 优点:理论基础扎实,在平衡点附近性能优越。
- 缺点:只在局部有效,全局性能可能不佳。
-
模型预测控制
- 原理:一种先进的优化控制方法,在每个控制周期,它会预测未来一段时间(预测时域)内系统的行为,并求解一个有限时域的优化问题,找到一系列最优控制输入,在下一周期,会重新进行预测和优化,形成滚动优化。
- 优点:能够显式处理各种约束(速度、加速度等),对模型不敏感,鲁棒性好,是目前高性能轨迹跟踪的主流方法。
- 缺点:计算复杂度较高,对处理器性能要求高。
两者的关系与协同工作
路径规划和轨迹跟踪是串联的关系,共同构成了机器人的运动控制系统。
典型的工作流程如下:
- 感知环境:机器人通过传感器(激光雷达、相机、IMU等)感知周围环境,构建或更新地图。
- 全局路径规划:基于全局地图和起点终点,使用A*或RRT等算法规划出一条全局参考路径。
- 局部路径规划/轨迹生成:
- 将全局路径分解为一系列短的路径段。
- 结合机器人的动力学约束和当前速度,为每个路径段生成一条平滑的时空轨迹,这条轨迹不仅包含位置,还包含每个时间点对应的速度和加速度,在直道上可以高速,在弯道上需要减速。
- 轨迹跟踪:
- 轨迹跟踪控制器(如MPC或纯追踪)以高频率(如100Hz)运行。
- 在每个控制周期,它获取机器人的当前状态(来自传感器),并与期望轨迹在当前时刻的状态进行比较。
- 根据误差,计算出下一时刻应该施加给电机的控制指令(
v, )。 - 机器人执行指令,实际运动。
- 循环与调整:
- 机器人持续感知环境,如果遇到新的障碍物或动态目标,局部路径规划器会重新规划,生成新的轨迹,传递给轨迹跟踪控制器。
- 这个过程不断循环,确保机器人安全、平滑地到达目的地。
| 特性 | 路径规划 | 轨迹跟踪 |
|---|---|---|
| 核心问题 | "走哪条路?" | "怎么走?" |
| 关注维度 | 空间 (2D/3D) | 时空 (空间+时间) |
| 输入 | 起点、终点、地图、障碍物 | 一条期望的轨迹 |
| 输出 | 一条几何路径 (点序列/曲线) | 控制指令 (速度 v, 角速度 ) |
| 主要方法 | A*, RRT, Dijkstra, 人工势场 | PID, 纯追踪, LQR, MPC |
| 关键挑战 | 避障、最优性、计算效率 | 模型不确定性、约束、鲁棒性 |
| 频率 | 较低 (Hz级别) | 较高 (几十到几百Hz) |
在实际应用中,路径规划和轨迹跟踪是一个密不可分的整体,一个优秀的路径规划器如果缺乏一个鲁棒的轨迹跟踪控制器,机器人也无法精确地执行任务,反之,即使跟踪控制器再好,如果规划的路径充满尖锐的转角或不切实际,机器人也无法实现平滑运动,二者的协同设计是实现机器人高性能自主导航的关键。
标签: 移动机器人路径轨迹协同优化算法 机器人路径规划与跟踪一体化控制 移动机器人动态路径轨迹协同调整
版权声明:除非特别标注,否则均为本站原创文章,转载时请以链接形式注明文章出处。