无人机基站侦查建模如何实现精准高效？

99ANYc3cd6 无人机 2025-12-07 8

问题定义与核心目标

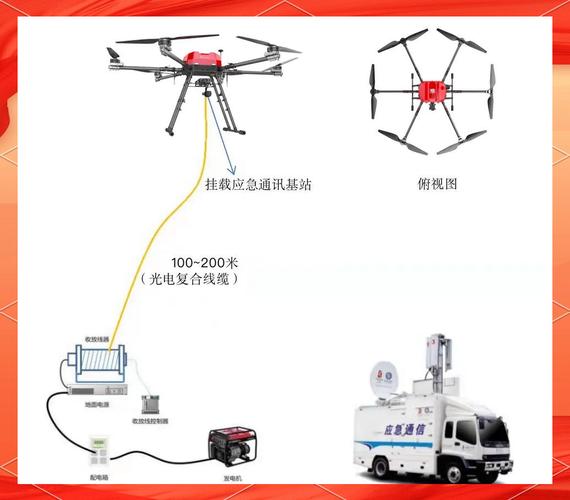
问题定义： 给定一个地理区域，区域内存在若干需要被侦查的地面基站（目标点），我们拥有一架或多架无人机，这些无人机可以作为移动的基站（通信中继或信号采集点），任务是为这些无人机规划最优的飞行路径和任务分配,使得对地面基站的侦查效果最大化。

（图片来源网络，侵删）

核心目标： 目标函数是最大化对地面基站的“侦查效能”，这个“效能”可以有多种量化方式,常见的有：

最大化覆盖的基站数量：在有限的飞行时间内，让无人机尽可能多地“看到”或“连接到”更多的基站。
最大化总侦查价值：每个基站有不同的优先级或价值（如基站的重要性、人流量等）,目标是让无人机覆盖的基站总价值最高。
最小化平均/最大侦查延迟：从任务开始到每个基站被成功侦查的时间,目标是让所有基站被侦查的速度尽可能快。
最大化信号质量：对于通信中继任务，目标是最大化所有被覆盖基站与无人机（或核心网）之间的信号质量总和（如信噪比SNR）。

约束条件：

无人机物理约束：
- 续航时间：无人机的总飞行时间不能超过其电池续航。
- 飞行速度：无人机的速度有上下限。
- 飞行高度：为了有效通信,无人机通常需要在最佳高度范围内飞行。
任务约束：
- 侦查时间：无人机在每个基站上需要停留一定时间进行数据采集或建立连接。
- 载荷能力：如果无人机需要携带特定设备,可能有重量限制。
通信约束：
- 覆盖范围：无人机与地面基站之间的通信距离不能超过其最大有效通信半径。
- 信道质量：信号质量会随距离、障碍物等衰减。
任务起始与终止：
- 起降点：无人机通常从一个或多个固定的基地起飞和降落。

核心要素与数学建模

为了将上述问题转化为数学模型,我们需要定义一些核心要素。

符号定义

集合:
- G = (V, E): 地面基站构成的图，V是基站顶点集，E是边集。
- U: 无人机集合。
- V₀: 无人机基地/起降点集合。
- V' = V ∪ V₀: 所有节点（基站和基地）的集合。
参数:
- N = |V|: 基站数量。
- M = |U|: 无人机数量。
- T_max^u: 无人机 u 的最大续航时间。
- v_u: 无人机 u 的飞行速度。
- t_ij: 从节点 i 飞行到节点 j 的时间，t_ij = d_ij / v_u，d_ij 是 i 和 j 之间的欧几里得距离。
- s_i: 在基站 i 的侦查时间。
- R_u: 无人机 u 的最大通信/侦查半径。
- w_i: 基站 i 的侦查价值。
- K_u: 无人机 u 的最大侦查基站数量。
决策变量:
- x_iju: 二元变量，如果无人机 u 从节点 i 飞往节点 j，则为1；否则为0。
- y_iu: 二元变量，如果无人机 u 侦查了基站 i，则为1；否则为0。
- t_iu: 连续变量，无人机 u 开始侦查基站 i 的时间。

目标函数

根据不同的核心目标,选择相应的目标函数。

（图片来源网络，侵删）

目标1：最大化总侦查价值 $$ \text{Maximize } Z = \sum{i \in V} \sum{u \in U} w_i \cdot y_iu $$
目标2：最小化最大侦查延迟 $$ \text{Minimize } Z = \max_{i \in V, u \in U} { t_iu + s_i } $$ （即所有基站中,最后一个被完成侦查的时间）

约束条件

这是一个典型的带时间窗的车辆路径问题的变种,约束条件非常丰富。

无人机起止约束:
- 每架无人机从一个基地出发，最终返回一个基地（可以是同一个）。
- $$ \sum{j \in V'} x{0ju} = 1, \quad \forall u \in U, 0 \in V_0 $$
- $$ \sum{i \in V'} x{i0u} = 1, \quad \forall u \in U, 0 \in V_0 $$
路径连续性约束 (Flow Conservation):
- 进入一个节点的无人机,必须从这个节点离开。
- $$ \sum{i \in V'} x{iju} = \sum{k \in V'} x{jku}, \quad \forall j \in V', u \in U $$
侦查覆盖约束:
（图片来源网络，侵删）
- 一个基站只能被一架无人机侦查。
- $$ \sum_{u \in U} y_iu \le 1, \quad \forall i \in V $$
路径与任务关联约束:
- 无人机只有在飞往某个基站时,才能侦查它。
- $$ \sum{j \in V'} x{iju} \le y_iu, \quad \forall i \in V, u \in U $$
- $$ \sum{i \in V'} x{iju} \le y_iu, \quad \forall i \in V, u \in U $$
时间窗与续航约束:
- 时间累积：无人机到达 j 的时间必须等于它从 i 出发的时间加上飞行时间。
  - $$ t_ju \ge t_iu + t_ij + si - M(1 - x{iju}) $$
  - （这是一个大M约束，当 x_{iju}=1 时，t_ju >= t_iu + t_ij + s_i；当 x_{iju}=0 时,约束无效）
- 续航限制：一架无人机所有飞行和侦查时间的总和不能超过其续航。
  - $$ \sum{i \in V'} \sum{j \in V'} tij \cdot x{iju} + \sum_{i \in V} s_i \cdot yiu \le T{max}^u, \quad \forall u \in U $$
通信范围约束:
- 无人机 u 只能在其通信半径 R_u 内侦查基站 i。
- y_iu = 1，则必须满足 d_iu <= R_u。
- 这个约束可以通过引入一个辅助变量或直接在求解器中处理，在数学模型中，可以这样体现：
  - 定义 d_iu 为无人机 u 与基站 i 的距离。
  - 在求解时，y_iu=1，则检查 d_iu <= R_u，如果违反，则该解不可行，或者，在构建邻接矩阵时，直接将 d_ij > R_u + R_v 的边 e=(u,v) 的权重设为无穷大,表示不可达。

求解算法

由于这是一个NP-Hard问题，对于大规模实例（基站和无人机数量多），精确算法（如分支定界法）在可接受时间内无法找到最优解,通常采用启发式或元启发式算法。

精确算法

适用场景：小规模问题（N < 20, M < 3）。
方法：使用商业求解器（如Gurobi, CPLEX）直接求解上述混合整数线性规划模型。
优点：能找到全局最优解。
缺点：计算时间随问题规模指数增长,不适用于实际大规模应用。

启发式算法

适用场景：中大规模问题,需要快速找到可行解。
方法：
- 贪婪算法：最近邻法，从基地出发，每次选择距离当前最近且未被侦查的基站，直到续航耗尽，然后派下一架无人机，简单快速,但解的质量通常不高。
- 节约算法：初始时每架无人机负责一个基站，然后尝试合并路径，如果合并后总时间不超过续航，则执行合并，并计算节约的成本（如总飞行距离减少）,迭代直到无法再合并。

元启发式算法

适用场景：大规模、复杂问题,需要在合理时间内找到高质量的近似最优解。
方法：
- 遗传算法:
  - 编码：将无人机的路径编码为一个染色体，一个染色体可以表示为 (U1_path, U2_path, ... Um_path)，U1_path = [基地, 基站3, 基站5, 基地]。
  - 适应度函数：目标函数（如总价值）或其变种。
  - 遗传操作：选择、交叉（交换两个解的部分路径）、变异（随机改变一个解的路径）。
  - 优点：全局搜索能力强,不易陷入局部最优。
  - 缺点：参数设置复杂,计算量较大。
- 蚁群优化:
  - 核心思想：模拟蚂蚁觅食，无人机（蚂蚁）在基站（食物源）之间移动，留下代表路径“好坏”的信息素，信息素浓度越高的路径,被后续无人机选择的概率越大。
  - 优点：正反馈机制能有效引导搜索,适合路径规划问题。
  - 缺点：收敛速度可能较慢,容易停滞。
- 模拟退火:
  - 核心思想：模拟金属退火过程，从一个随机解开始，随机产生一个邻域解，如果新解更好，则接受；如果新解更差，则以一定的概率（随“温度”降低而减小）接受。
  - 优点：能有效跳出局部最优。
  - 缺点：需要精心设计邻域结构和冷却策略。

扩展与高级模型

多无人机协同:
- 无人机可以协同覆盖一个区域,形成一个动态的通信网络。
- 建模：需要引入无人机之间的通信链路，可能需要考虑网络连通性约束,即所有被无人机覆盖的区域或无人机本身需要形成一个连通图。
动态环境:
- 考虑基站位置、通信需求或天气条件随时间变化。
- 建模：这变成了一个动态路径规划问题，需要在每个时间步（或事件发生时）重新规划路径，可以使用滚动时域优化方法，即在每个决策点只规划未来一段时间的路径，执行一段时间后,再根据最新的环境信息进行下一次规划。
3D空间与障碍物:
- 考虑地形起伏和禁飞区（建筑物、高山等）。
- 建模：节点空间从2D扩展到3D，邻接矩阵 E 需要重构，只有两点之间无障碍物直线路径时，才存在边，这通常需要结合路径规划算法（如A、RRT）来生成可行的飞行路径段。