机器人路径规划MATLAB怎么实现？

99ANYc3cd6 机器人 2025-12-06 10

核心概念简介
（图片来源网络，侵删）
- 工作空间与环境建模
- 自由空间与障碍物
- 路径 vs. 轨迹
- 主要算法分类
MATLAB 仿真环境准备
- 必要工具箱
- 创建地图（栅格地图法）
经典路径规划算法 MATLAB 实现
- 案例 1：A* 算法 - 基于栅格图的启发式搜索
- 案例 2：RRT (Rapidly-exploring Random Tree) 算法 - 基于采样的随机探索
- 案例 3：PRM (Probabilistic Roadmap) 算法 - 基于采样的概率路图
高级与专业工具箱
- Robotics System Toolbox™
- Navigation Toolbox™
完整示例代码与可视化
（图片来源网络，侵删）

核心概念简介

在开始编码前,理解几个基本概念很重要：

工作空间与环境建模：机器人可以活动的区域，在 MATLAB 中，我们通常用一个二维或三维的栅格来表示，每个格子要么是“自由空间”，要么是“障碍物”。
自由空间与障碍物：路径规划的目标是在自由空间中找到一条从起点到终点的路径，同时避开所有障碍物。
路径 vs. 轨迹：
- 路径：是机器人位置点的序列，只关心“经过哪里”，不关心“何时到达”和“速度如何”。
- 轨迹：是路径加上时间信息，即 位置 = f(时间)，它包含了速度、加速度等动态约束，本指南主要关注路径规划。
主要算法分类：
- 基于图的搜索：如 A*、Dijkstra，将环境离散化为图节点，通过搜索算法找到最优路径。
- 基于采样的方法：如 RRT、PRM，在自由空间中随机采样点，并连接它们构建路径树或路图，适合高维或复杂环境。
- 基于人工势场：将目标点视为“引力”，障碍物视为“斥力”，机器人在这两种力的作用下移动，简单但可能陷入局部最优。

MATLAB 仿真环境准备

必要工具箱

MATLAB®：基础平台。
Robotics System Toolbox™：提供了机器人学相关的数据结构（如 robotics.Polyhedron）、运动学求解器、地图表示等，是进行仿真的利器。
Navigation Toolbox™：专门用于导航的高级工具箱，集成了路径规划、传感器融合、地图构建等功能，极大地简化了开发流程。

创建地图（栅格地图法）

最常用的方法是创建一个二维矩阵（栅格图）来表示环境。

0 或 false：表示自由空间
1 或 true：表示障碍物

示例：创建一个简单的地图

% 定义地图大小
mapWidth = 50;  % 格子数
mapHeight = 50;
% 初始化一个全为0（自由空间）的地图
map = zeros(mapHeight, mapWidth);
% 添加一些矩形障碍物
% 障碍物1
map(10:20, 15:25) = 1;
% 障碍物2 (L型)
map(30:40, 10:20) = 1;
map(30:35, 20:30) = 1;
% 障碍物3
map(5:15, 35:45) = 1;
% 可视化地图
figure;
imshow(map, 'InitialMagnification', 'fit');'机器人工作空间地图');
xlabel('X (格子)');
ylabel('Y (格子)');
colorbar; % 显示颜色条，0是蓝色，1是白色

经典路径规划算法 MATLAB 实现

我们将手动实现前两种最经典的算法,以理解其核心思想。

（图片来源网络，侵删）

**案例 1：A* 算法**

A* 算法是一种广泛使用的路径搜索算法，它通过评估每个节点的代价 f(n) = g(n) + h(n) 来决定搜索方向。

g(n)：从起点到当前节点 n 的实际代价。
h(n)：从当前节点 n 到终点的预估代价（启发式函数），通常用曼哈顿距离或欧几里得距离。

实现步骤：

定义地图、起点、终点。
定义搜索的 8 个可能移动方向（上、下、左、右、左上、右上、左下、右下）。
初始化开放列表（待探索节点）和关闭列表（已探索节点）。
将起点加入开放列表。
循环直到开放列表为空或找到终点： a. 从开放列表中取出 f(n) 值最小的节点作为当前节点。 b. 将当前节点移入关闭列表。 c. 如果当前节点是终点，则回溯构建路径。 d. 否则，遍历当前节点的所有邻居： i. 如果邻居是障碍物或在关闭列表中，则跳过。 ii. 计算邻居的 g(n) 和 h(n) 值。 iii. 如果邻居不在开放列表中，或找到一条更优的路径（g(n) 更小），则更新邻居信息并将其加入开放列表。

MATLAB 代码实现：

% --- A* 算法实现 ---
% 1. 准备地图和参数
map = [ ... ]; % 使用上面创建的地图
start = [5, 5];   % 起点坐标 [y, x]
goal = [45, 45]; % 终点坐标 [y, x]
% 2. 定义参数
% 8个可能移动方向 (dy, dx)
directions = [...
    -1, 0;  % 上
     1, 0;  % 下
     0, -1; % 左
     0, 1;  % 右
    -1, -1; % 左上
    -1, 1;  % 右上
     1, -1; % 左下
     1, 1]; % 右下
% 每个方向的移动代价
% 对角线移动代价为 sqrt(2)，直线为 1
moveCost = [1.0; 1.0; 1.0; 1.0; 1.414; 1.414; 1.414; 1.414];
% 3. 初始化数据结构
[rows, cols] = size(map);
% gScore: 从起点到每个点的实际代价
gScore = inf(rows, cols);
gScore(start(1), start(2)) = 0;
% fScore: gScore + 启发式函数值
fScore = inf(rows, cols);
fScore(start(1), start(2)) = heuristic(start, goal);
% openSet: 待探索的节点，使用优先队列模拟，这里用矩阵和find来简化
openSet = false(rows, cols);
openSet(start(1), start(2)) = true;
% cameFrom: 记录路径
cameFrom = zeros(rows, cols, 2);
% 4. 主循环
while any(openSet(:))
    % 找到 fScore 最小的节点
    [minFScore, idx] = min(fScore(openSet));
    [currentY, currentX] = ind2sub([rows, cols], find(openSet, 1, 'first'));
    % 如果到达终点
    if isequal([currentY, currentX], goal)
        path = reconstructPath(cameFrom, currentY, currentX);
        break;
    end
    % 将当前节点从开放列表移除
    openSet(currentY, currentX) = false;
    % 遍历邻居
    for i = 1:size(directions, 1)
        neighborY = currentY + directions(i, 1);
        neighborX = currentX + directions(i, 2);
        % 检查邻居是否有效
        if neighborY < 1 || neighborY > rows || neighborX < 1 || neighborX > cols
            continue;
        end
        if map(neighborY, neighborX) == 1 % 是障碍物
            continue;
        end
        % 计算从起点到邻居的临时 gScore
        tentative_gScore = gScore(currentY, currentX) + moveCost(i);
        % 如果这条路径更好
        if tentative_gScore < gScore(neighborY, neighborX)
            cameFrom(neighborY, neighborX, :) = [currentY, currentX];
            gScore(neighborY, neighborX) = tentative_gScore;
            fScore(neighborY, neighborX) = tentative_gScore + heuristic([neighborY, neighborX], goal);
            openSet(neighborY, neighborX) = true;
        end
    end
end
% 如果循环结束仍未找到路径
if ~isequal(path(end, :), goal)
    disp('未找到可行路径！');
    path = [];
end
% --- 辅助函数 ---
% 启发式函数（曼哈顿距离）
function h = heuristic(pos1, pos2)
    h = abs(pos1(1) - pos2(1)) + abs(pos1(2) - pos2(2));
end
% 回溯路径
function path = reconstructPath(cameFrom, currentY, currentX)
    path = [currentY, currentX];
    while true
        parent = cameFrom(currentY, currentX, :);
        if isequal(parent, [0, 0])
            break;
        end
        path = [parent; path];
        [currentY, currentX] = deal(parent(1), parent(2));
    end
end
% --- 可视化 ---
figure;
imshow(map, 'InitialMagnification', 'fit');
hold on;
% 绘制起点和终点
plot(start(2), start(1), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');
plot(goal(2), goal(1), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
% 绘制路径
if ~isempty(path)
    plot(path(:, 2), path(:, 1), 'y-', 'LineWidth', 2);
end
'A* 算法路径规划结果');
legend('地图', '起点', '终点', '规划路径');
xlabel('X (格子)');
ylabel('Y (格子)');

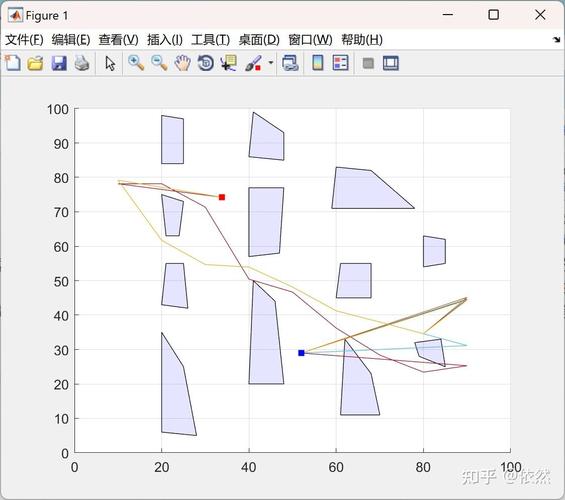
案例 2：RRT (Rapidly-exploring Random Tree) 算法

RRT 是一种非常适合高维空间和复杂障碍物环境的算法，它从一个初始节点开始，不断向随机方向扩展，直到找到目标。

实现步骤：

初始化一棵树,只包含起点。
循环直到找到路径或达到最大迭代次数： a. 在工作空间中随机采样一个点 q_rand。 b. 在树中找到距离 q_rand 最近的节点 q_near。 c. 从 q_near 向 q_rand 方向延伸一个固定步长 step_size，得到新节点 q_new。 d. q_new 和 q_near 之间的路径不与障碍物碰撞，则将 q_new 添加到树中，并记录其父节点。 e. （可选）q_new 距离目标足够近，则直接连接到目标，算法成功。

MATLAB 代码实现：

% --- RRT 算法实现 ---
% 1. 准备地图和参数
map = [ ... ]; % 使用上面创建的地图
start = [5, 5];   % 起点坐标 [y, x]
goal = [45, 45]; % 终点坐标 [y, x]
goalRegion = 2;  % 目标点半径（格子数）
maxIterations = 5000;
stepSize = 2;    % 每次扩展的步长（格子数）
% 2. 初始化树
nodes = start; % 节点坐标 [y, x]
parentIndices = 1; % 每个节点的父节点索引，根节点的父节点是自己
% 3. 主循环
for i = 2:maxIterations
    % a. 随机采样
    if rand() < 0.1 % 10%的概率直接采样目标点，加速收敛
        q_rand = goal;
    else
        q_rand = [randi(size(map, 1)), randi(size(map, 2))];
    end
    % b. 找到最近的节点
    distances = sqrt(sum((nodes - q_rand).^2, 2));
    [~, idx_near] = min(distances);
    q_near = nodes(idx_near, :);
    % c. 扩展新节点
    direction = q_rand - q_near;
    direction = direction / norm(direction); % 单位化
    q_new = round(q_near + direction * stepSize);
    % 确保新节点在地图范围内
    q_new(1) = max(1, min(size(map, 1), q_new(1)));
    q_new(2) = max(1, min(size(map, 2), q_new(2)));
    % d. 检查碰撞
    if isPathCollisionFree(q_near, q_new, map)
        % 添加新节点
        nodes = [nodes; q_new];
        parentIndices = [parentIndices; idx_near];
        % e. 检查是否到达目标
        if norm(q_new - goal) < goalRegion
            disp('RRT 找到路径！');
            % 回溯构建完整路径
            pathIndices = findPathToGoal(nodes, parentIndices, q_new);
            path = nodes(pathIndices, :);
            break;
        end
    end
end
if i == maxIterations
    disp('RRT 达到最大迭代次数仍未找到路径。');
    path = [];
end
% --- 辅助函数 ---
% 检查两点之间的线段是否与障碍物碰撞
function isCollision = isPathCollisionFree(q1, q2, map)
    % 使用 Bresenham 算法获取线段上的所有点
    points = bresenham_line(q1(1), q1(2), q2(1), q2(2));
    % 检查这些点是否都是自由空间
    isCollision = any(map(points(:, 1), points(:, 2)) == 1);
end
% Bresenham 直线算法
function points = bresenham_line(y0, x0, y1, x1)
    points = [];
    dx = abs(x1 - x0);
    dy = abs(y1 - y0);
    sx = x0 < x1 ? 1 : -1;
    sy = y0 < y1 ? 1 : -1;
    err = dx - dy;
    while true
        points = [points; y0, x0];
        if x0 == x1 && y0 == y1, break; end
        e2 = 2 * err;
        if e2 > -dy
            err = err - dy;
            x0 = x0 + sx;
        end
        if e2 < dx
            err = err + dx;
            y0 = y0 + sy;
        end
    end
end
% 回溯到目标节点的路径
function pathIndices = findPathToGoal(nodes, parentIndices, goalNode)
    pathIndices = [];
    currentIdx = find(ismember(nodes, goalNode, 'rows'), 1);
    while currentIdx ~= 0
        pathIndices = [currentIdx, pathIndices];
        if currentIdx == 1 % 到达根节点
            break;
        end
        currentIdx = parentIndices(currentIdx);
    end
end
% --- 可视化 ---
figure;
imshow(map, 'InitialMagnification', 'fit');
hold on;
% 绘制起点和终点
plot(start(2), start(1), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');
plot(goal(2), goal(1), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
% 绘制目标区域
rectangle('Position', [goal(2)-goalRegion, goal(1)-goalRegion, 2*goalRegion, 2*goalRegion], 'EdgeColor', 'r', 'LineWidth', 2, 'LineStyle', '--');
% 绘制树
for i = 2:size(nodes, 1)
    parent_node = nodes(parentIndices(i), :);
    child_node = nodes(i, :);
    plot([parent_node(2), child_node(2)], [parent_node(1), child_node(1)], 'c-', 'LineWidth', 0.5);
end
% 绘制最终路径
if ~isempty(path)
    plot(path(:, 2), path(:, 1), 'y-', 'LineWidth', 3);
end
'RRT 算法路径规划结果');
legend('地图', '起点', '终点/目标区', '探索树', '规划路径');
xlabel('X (格子)');
ylabel('Y (格子)');

高级与专业工具箱

手动实现算法有助于理解原理,但在实际项目中，使用 MathWorks 提供的专业工具箱会更高效、更可靠。

Robotics System Toolbox™

提供了 occupancyMap 类来表示占据栅格地图，并内置了 pathplanner 对象，支持 A* 和 RRT 算法。

示例：使用 Robotics System Toolbox

% 1. 创建占据栅格地图
map = occupancyMap(zeros(50, 50));
% 添加障碍物
setOccupancy(map, 10:20, 15:25, 1);
setOccupancy(map, 30:40, 10:20, 1);
setOccupancy(map, 30:35, 20:30, 1);
setOccupancy(map, 5:15, 35:45, 1);
% 2. 创建路径规划器
planner = pathPlanner(map, 'MaxIterations', 10000, 'Resolution', 1); % Resolution是地图每个格子的大小
% 3. 设置起点和终点
start = [5, 5];
goal = [45, 45];
% 4. 规划路径
[path, distance] = planner.plan(start, goal);
% 5. 可视化
show(planner);
hold on;
plot(start(1), start(2), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');
plot(goal(1), goal(2), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
plot(path(:, 1), path(:, 2), 'y-', 'LineWidth', 2);
hold off;'Robotics System Toolbox - A* / RRT 路径规划');

Navigation Toolbox™

这是更高级的工具箱,专注于完整的导航任务，它提供了 plannerRRT 和 plannerAStar 等类，并且可以与 costmap（代价地图）配合使用，考虑机器人宽度等更复杂的约束。

总结与建议

方法	优点	缺点	适用场景
*手动实现 (A/RRT)**	深入理解算法原理，灵活性高	代码量大，需要处理细节（如碰撞检测），可能不够鲁棒	学术研究，教学，或需要高度定制化的特殊场景
Robotics System Toolbox	高度封装，API简单，可靠，支持多种规划器	需要购买工具箱	快速原型开发，标准机器人应用
Navigation Toolbox	功能最全，支持代价地图、动态环境等高级导航功能	需要购买工具箱，学习曲线稍陡	完整的自主导航系统开发，SLAM, 避障等

给你的建议：

从手动实现开始：如果你是初学者，强烈建议先尝试手动实现 A* 或 RRT，这会帮助你打下坚实的基础，理解算法的每一步是如何工作的。
学习专业工具箱：当你理解了基本原理后，转向 Robotics System Toolbox，你会发现用几行代码就能实现复杂的规划，这是工程实践中最高效的方式。
探索高级功能：如果项目需求更复杂（如考虑机器人运动学、动态障碍物等），再深入了解 Navigation Toolbox。

希望这份详细的指南能帮助你顺利入门 MATLAB 机器人路径规划！祝你学习愉快！

标签：机器人路径规划MATLAB代码 MATLAB机器人路径规划算法实现机器人路径规划MATLAB仿真